9. November 2011
Saving the Parrots with Homogeneous Coordinates
 A well-known result from linear algebra is that one can use a matrix to represent any linear mapping between two vector spaces. While rotation is a linear mapping, translation unfortunately is not. But, wait… by adding another dimension to the vector space, and by interpreting the vector coordinates correctly, we are able to perform rotation and translation with a single matrix multiplication! This article describes how to restore a fragmented image with the help of homogeneous coordinates.
A well-known result from linear algebra is that one can use a matrix to represent any linear mapping between two vector spaces. While rotation is a linear mapping, translation unfortunately is not. But, wait… by adding another dimension to the vector space, and by interpreting the vector coordinates correctly, we are able to perform rotation and translation with a single matrix multiplication! This article describes how to restore a fragmented image with the help of homogeneous coordinates.
Here is a 600×300 image of two parrots (scaled for display).

Imagine this image gets fragmented into two pieces, each 300×300 pixels. Both fragments are translated and rotated and become part of the following larger image (scaled for display):

In this example, our task shall be to reconstruct the original image. The three degrees of freedom for translation and rotation (for each fragment) shall be determined by the user; s/he needs to select the upper left corner and the upper right corner of each fragment.
Consider just the left fragment (the right one is treated in the same way). A coordinate system is attached to the upper left corner (Q) of the fragment. Its coordinates are denoted as (u, v) where the u-axis points rightwards and the v-axis points downwards.
The second coordinate system is the coordinate system whose origin is the absolute upper left corner (P) of an image shown on the screen. The user effectively selects the points Q and U. This being done, we can calculate the angle of rotation and the translation vector
Using the four-quadrant inverse tangent atan2,
we compute the angle between x-axis and u-axis:
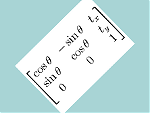
Then we can define a transformation matrix using homogeneous coordinates:
So for every point (x, y) we can calculate (u, v) with a single matrix multiplication:
What remains to do is to turn the maths into an implementation. Bilinear interpolation helps to make the restored image look better. Here is the corresponding Matlab demo for restoring parrots with translation and rotation using homogeneous coordinates.
See also: Hartley, R. and Zissermann, A., “Multiple View Geometry”, 2nd ed., p. 1ff.