8. März 2020
Modeling Swiss basic health insurance
 In this article, I am reverse-engineering the Swiss healthcare system, with the help of some maths and diagrams. In particularly, I am looking at the impact of the deductible when buying a basic insurance policy. How much difference does the choice of deductible make?
In this article, I am reverse-engineering the Swiss healthcare system, with the help of some maths and diagrams. In particularly, I am looking at the impact of the deductible when buying a basic insurance policy. How much difference does the choice of deductible make?
In this article, I want to illustrate how Swiss health insurance works, and in particularly present a model that has helped me to understand some of the choices when selecting one of the many insurance policies available on the market. There is already good quality documentation about how Swiss health insurance works on the Internet, such as https://www.ch.ch/en/health-insurance, for example. But how do I predict some of the consequences of my choices? How do I make sure I really understand the links between important concepts involved, such as premium, deductible, copayment? By visualizing these links.
Let’s get started by introducing the concepts. In a nutshell, Switzerland requires everyone to be covered by basic insurance, which guarantees certain access to healthcare (on top of the basic insurance, you can purchase supplementary insurance, but that is out of scope in this article). For the insurance policy, the policyholder pays a monthly premium to the insurance provider.
Over the course of a year, the policyholder consumes healthcare services (doctor visits, prescriptions, etc) that ultimately need to be footed by either the insured or the insurance, regardless of the particular settlement scheme. I will only include healthcare services here that are covered by the basic insurance. For the annual cost for these healthcare services accrued in excess of the deductible for the policy, the policyholder is responsible for paying a fraction─the so-called copayment ─of the costs up until a maximum copayment, whereas (what I call) insurance provider contributions will cover the rest. The policyholder must pay the annual cost up to the deductible in full. In summary, the costs for the healthcare services consumed are paid by the sum of (what I call) policyholder contributions and insurance provider contributions.
Got it? If not, don’t worry. It took me a long time to arrive at a solid conceptual model. And part of why I looked into visualizing these concepts and the relationships in the first place was because it took me such a long time without doing so in the first place! Once you have understand how it works, then (at least the basics as covered in this article) things are simple and you might wonder why they appeared difficult in the first place. But such it is with all learning processes, things look difficult first, then you plough through the material, and then everything starts making sense..
So let’s summarize what concepts we have, and in particular, introduce some variables, formalizing the model just described. You can skip this section, as it is redundant, but I like having the relationships expressed as equations:
- H: (annual) cost for healthcare services [CHF]
- P: (annual) policyholder contribution [CHF]
- I: (annual) insurance provider contribution [CHF]
- PD: (annual) policyholder contribution due to deductible [CHF]
- PC: (annual) policyholder contribution due to copayment [CHF]
- PC,max: (annual) max. policyholder contribution due to copayment [CHF]
- D: deductible as defined in the insurance policy [CHF]
- C: copayment, 10% [CHF]
- MD: monthly premium paid by the policyholder [CHF]
- E: (annual) net expense for policyholder
The annual costs for healthcare services are either paid by the policyholder or by the insurance:
The policyholder has to make contributions due to the deductible, and the due to copayment: . The contribution due to the deductible cannot exceed the cost of healthcare services, thus
. The contribution due to copayment is zero unless the cost of healthcare services exceeds the deductible, and the contribution due to copayment is capped, so
.
Finally, as a policyholder, you care about your health first, and then about everything that you have to pay related to it, i.e. the monthly premiums and the contribution to the costs for healthcare services consumed: , or equivalently:
. Substituting PD and PC, we obtain the formula to compute the annual net expenses for the policyholder:
What have we got? As a policyholder, I can look at the formula and understand what influences the annual net expense. Most importantly, the expenses are a function non-linear in the chosen deductible and the healthcare services consumed over the course of a year. The monthly premium depends on the deductible (insurance policy providers reduce the premium if you choose a higher deductible). And then there are your policyholder contributions, which depend non-linearly on both deductible and healthcare services consumed. After all, what we want is to choose the deductible which minimizes our net expense:
If that function was linear and if we were able to accurately predict how much healthcare services we are going to consume in the years to come, then we had a much easier time choosing the right deductible.
What I will do in the remaining part of this article is to visualize what happens to your net expenses if you choose a deductible given a particular consumption (cost) of healthcare services, or alternatively, look at different scenarios for healthcare service consumption given a particular insurance policy. At the very least, answering these two questions shall help form a basic understanding of what consequences our choices in basic insurance policy have.
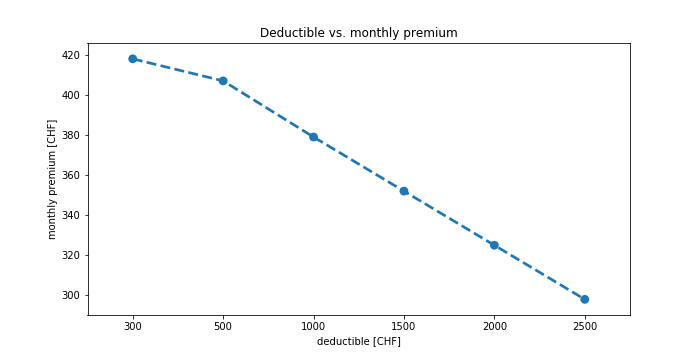
To get some real data, I picked one of the large health insurance providers in Switzerland and here is the offers for basic insurance packages, with the monthly premium depending on the chosen deductible:
| Deductible | Monthly premium |
|---|---|
| 300 | 418 |
| 500 | 407 |
| 1000 | 379 |
| 1500 | 352 |
| 2000 | 325 |
| 2500 | 298 |
When plotting the deductible against the associated monthly premium, we can clearly see that the bigger the deductible you choose, the smaller the monthly premium. This is not super useful by itself, of course.
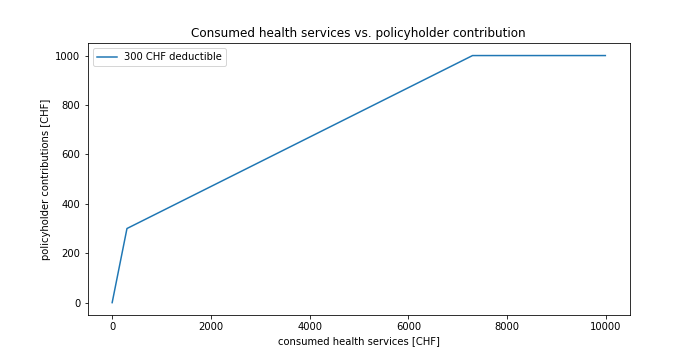
How does your contribution to the annual “doctor’s bill” change, depending on the size of the bill? Let’s first start with a deductible of 300 CHF. There are three different regimes. First, you have to foot the doctor’s bill yourself all until you reach the deductible. Second, you have to contribute a fraction of the cost in excess of the deductible (that’s the copayment). Third, beyond a certain cost, the insurance pays everything (which is the point of insurance: to insure you against unlimited or existential loss).
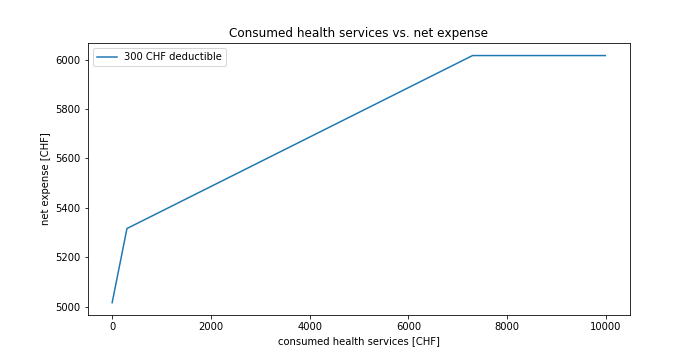
Or showing the net expense (i.e. policyholder contributions and premiums):
How does your net expense (remember: both premiums and contribution) change, depending on the deductible you choose and depending on the size of the annual “doctor’s bill”? Let’s have a look:
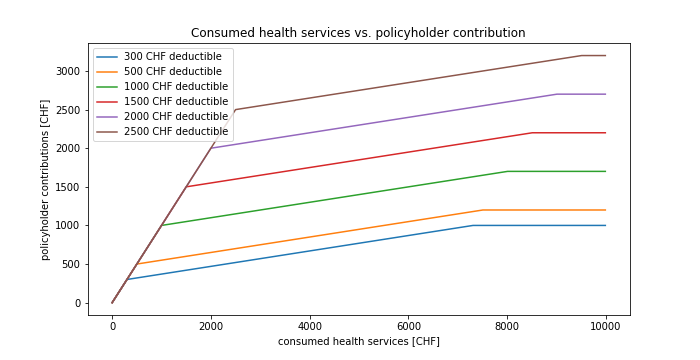
Or showing the net expense (i.e. policyholder contributions and premiums). The diagram below is the most interesting one:

What is the impact of the deductible on the net expense? Let us define impact as the maximum difference the choice of deductible has on the net expense, i.e. the maximum savings we could achieve by choosing the right deductible, or the maximum loss you could sustain by choosing the wrong deductible. Depending on how you look at it.

For this particular insurance provider, we can see that the choice of deductible has the most impact when the annual costs for healthcare service are low (0-2500 CHF). We can thus infer─assuming we would only have a policy for one year─that choosing the worst deductible cannot cost us more than 1440 CHF. Or positively formulated, choosing the right deductible could save us up to 1440 CHF. But no more. From 2500-7300 CHF, the range in net expenses is only 540 CHF, so it makes less of a difference which deductible you chose. From 7300 CHF and above, the range in net expenses goes up to 760 CHF, so the impact of the deductible grows again.

Given what we now learnt about the impact of the deductible, how do we choose a deductible? Clearly, to make the ideal choice we must know the probabilities for how large the “doctor’s bill” is going to be. These probabilities are hard to estimate. But the probabilities are key. We don’t know the probabilities, but one probability that we might want to estimate in the example at hand is how likely is the doctor’s bill smaller than CHF 2000 and how likely is the doctor’s bill smaller than CHF 1000?
I hope that this exercise was useful to you as it was for me. Download the code for the model and the visualizations as a Colab notebook if you are interested. I have written the above content to the best of my knowledge. Feedback welcome.