The Viterbi Algorithm and Breadth-First Search

A short review of the problem: we are given a hidden Markov model (HMM) with N states and a sequence of T observations. The sequence of T states that generated those observations is latent. We want to find the most likely state sequence given the observations.

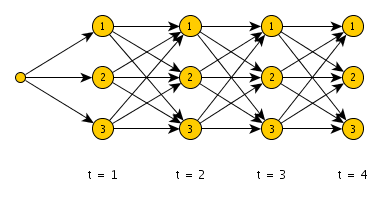
As an example, let us suppose we observed T=4 values. Each of these values emanated from one of altogether N=3 states. Then, as shown in the graph above, the task is to find the most likely sequence of states. We can find it by comparing the likelihoods of all N^T=81 possible state sequences. The figure above shows all the possible paths – nodes represent the state of the process at certain times. We can actually unwrap this graph into a perfect 3-ary tree of depth 4.

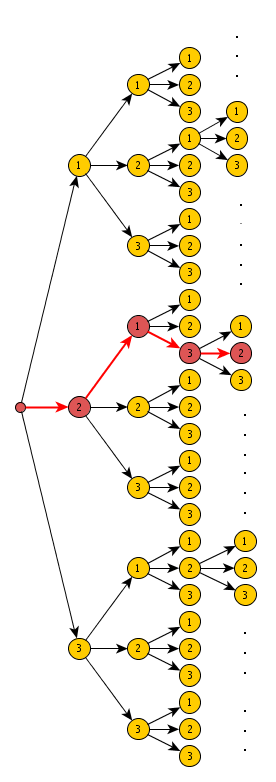
Exhaustively searching the tree in the figure above lets us find the most likely state sequence. Fortunately, we do not have to search the whole tree. If we proceed in a breadth-first search (BFS) strategy, then we only need to expand N nodes at each tree level. Why? Well, the MAP state sequence has the nice property that the sub-sequences of states until time t <= T are also MAP sequences for the corresponding sequence of observations. Hence, we need only consider a single path for each state at time t while searching for the MAP sequence, and can safely discard all other paths.

Formulating the Viterbi algorithm in terms of breadth-first search is beneficial, as breadth-first search is well-known. I learned first about this connection from Dekai Wu (HKUST), who pointed out in a lecture that it is a little bit strange to give this algorithm a special name. It was not until I took a pattern recognition course by Arne Leijon (KTH) before I had the equipment to base these insights on the Viterbi algorithm a.k.a. breadth-first search on solid grounds.